题目

编号： 201803-2

试题名称： 碰撞的小球

时间限制： 1.0s

内存限制： 256.0MB

问题描述

数轴上有一条长度为L（L为偶数)的线段，左端点在原点，右端点在坐标L处。有n个不计体积的小球在线段上，开始时所有的小球都处在偶数坐标上，速度方向向右，速度大小为1单位长度每秒。
当小球到达线段的端点（左端点或右端点）的时候，会立即向相反的方向移动，速度大小仍然为原来大小。
当两个小球撞到一起的时候，两个小球会分别向与自己原来移动的方向相反的方向，以原来的速度大小继续移动。
现在，告诉你线段的长度L，小球数量n，以及n个小球的初始位置，请你计算t秒之后，各个小球的位置。

提示

因为所有小球的初始位置都为偶数，而且线段的长度为偶数，可以证明，不会有三个小球同时相撞，小球到达线段端点以及小球之间的碰撞时刻均为整数。
同时也可以证明两个小球发生碰撞的位置一定是整数（但不一定是偶数）。

输入格式

输入的第一行包含三个整数n, L, t，用空格分隔，分别表示小球的个数、线段长度和你需要计算t秒之后小球的位置。
第二行包含n个整数$a_1, a_2, \dots, a_n$，用空格分隔，表示初始时刻n个小球的位置。

输出格式

输出一行包含n个整数，用空格分隔，第i个整数代表初始时刻位于$a_i$的小球，在t秒之后的位置。

样例数据

样例输入1

1 2	3 10 5 4 6 8

样例输出1
7 9 9

样例说明1
初始时，三个小球的位置分别为4, 6, 8。

一秒后，三个小球的位置分别为5, 7, 9。

两秒后，第三个小球碰到墙壁，速度反向，三个小球位置分别为6, 8, 10。

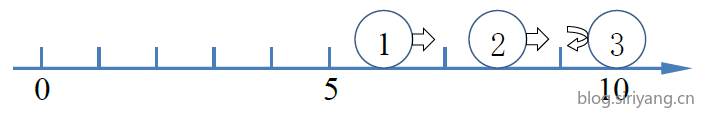
三秒后，第二个小球与第三个小球在位置9发生碰撞，速度反向（注意碰撞位置不一定为偶数），三个小球位置分别为7, 9, 9。

四秒后，第一个小球与第二个小球在位置8发生碰撞，速度反向，第三个小球碰到墙壁，速度反向，三个小球位置分别为8, 8, 10。

五秒后，三个小球的位置分别为7, 9, 9。

样例输入2

1 2	10 22 30 14 12 16 6 10 2 8 20 18 4

样例输出2
6 6 8 2 4 0 4 12 10 2

数据规模和约定

对于所有评测用例，1 $\le$ n $\le$ 100，1 $\le$ t $\le$ 100，2 $\le$ L $\le$ 1000，0 < $a_i$ < L。L为偶数。
保证所有小球的初始位置互不相同且均为偶数。

解答

分析

使用ball数组来存储每个球的状态，ball[i][0]表示球的位置，ball[i][1]表示球运动的方向，1为向右，-1为向左。循环t秒，每一秒都模拟更新球的位置，遇到边界就改变球的运动方向。当所有球都运动一秒后再两辆对比两个球的位置，若两个球的位置相同就分别改变他们的运动方向。

代码

#include <iostream>

using namespace std;

int main() {

	int n,L,t;
	int ball[1001][2];

	cin >> n >> L >> t;

	for (int i = 0; i < n; i++) {
		cin >> ball[i][0];
		ball[i][1] = 1;
	}

	for (int i = 0; i < t; i++) {
		for (int j = 0; j < n; j++) {
			if (ball[j][0] == 0 || ball[j][0] == L) 
				ball[j][1] *= -1;
			ball[j][0] += ball[j][1];
		}

		for (int k = 0; k < n; k++) 
			for (int l = k+1; l < n; l++)
			if (ball[k][0] ==  ball[l][0] ) {
				ball[k][1] *= -1;
				ball[l][1] *= -1;
			}
	}

	for (int j = 0; j < n; j++) {
		cout<<ball[j][0]<<" ";
	}

	return 0;
}