X-Data数据工程基础实践（三）

发表于 更新于 分类于 ， 阅读次数： Valine：
本文字数： 8.8k 阅读时长 ≈ 8 分钟

前言

  KMeans算法本身说起来还算简单，但具体实现起来还是不容易啊。

正文

  今天来完成任务一的实验四：实现Kmeans算法，并测试5个数据集。

代码

  要导入的包有：

1
2
3
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

工具函数

  懒得去找数据集了，还是使用随机数生成：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
if __name__ == "__main__":
   data=np.random.rand(100)*100

   data.resize((50,2))

   plt.scatter(data[:,0],data[:,1])
   plt.show()

   d={'X':pd.Series(data[:,0]),
      'Y':pd.Series(data[:,1])}

   df=pd.DataFrame(d)

   df.to_csv("./testdata.csv", encoding="utf-8-sig", header=True, index=False)

  接下来的两个函数在之后的寻找K和计算聚类都会用到。
  根据数据集和选取的K值随机生成k个初始点：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
def randCent(dataMat, k):
    '''
    为给定数据集构建一个包含K个随机质心的集合,
    随机质心必须要在整个数据集的边界之内,这可以通过找到数据集每一维的最小和最大值来完成
    然后生成0到1.0之间的随机数并通过取值范围和最小值,以便确保随机点在数据的边界之内
    :param dataMat:
    :param k:
    :return:
    '''
    # 获取样本数与特征值
    m, n = np.shape(dataMat)
    # 初始化质心,创建(k,n)个以零填充的矩阵
    centroids = np.mat(np.zeros((k, n)))
    # 循环遍历特征值
    for j in range(n):
        # 计算每一列的最小值
        minJ = min(dataMat[:, j])
        # 计算每一列的范围值
        rangeJ = float(max(dataMat[:, j]) - minJ)
        # 计算每一列的质心,并将值赋给centroids
        centroids[:, j] = np.mat(minJ + rangeJ * np.random.rand(k, 1))
    # 返回质心
    return centroids

  计算欧式距离：

1
2
3
4
5
6
7
8
def distEclud(vecA, vecB):
    '''
    欧氏距离计算函数
    :param vecA:
    :param vecB:
    :return:
    '''
    return np.sqrt(np.sum(np.power(vecA - vecB, 2)))

findBestK

  首先确定该数据集K的最佳取值：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
def cost(dataMat, k, distMeas=distEclud, createCent=randCent,iterNum=300):
    '''
    计算误差的多少，通过这个方法来确定 k 为多少比较合适，这个其实就是一个简化版的 kMeans
    :param dataMat: 数据集
    :param k: 簇的数目
    :param distMeans: 计算距离
    :param createCent: 创建初始质心
    :param iterNum：默认迭代次数
    :return:
    '''
    # 获取样本数和特征数
    m, n = np.shape(dataMat)
    # 初始化一个矩阵来存储每个点的簇分配结果
    # clusterAssment包含两个列:一列记录簇索引值,第二列存储误差(误差是指当前点到簇质心的距离,后面会使用该误差来评价聚类的效果)
    clusterAssment = np.mat(np.zeros((m, 2)))
    # 创建质心,随机K个质心
    centroids = createCent(dataMat, k)
    clusterChanged = True
    while iterNum > 0:
        clusterChanged = False
        # 遍历所有数据找到距离每个点最近的质心,
        # 可以通过对每个点遍历所有质心并计算点到每个质心的距离来完成
        for i in range(m):
            minDist = np.inf
            minIndex = -1
            for j in range(k):
                # 计算数据点到质心的距离
                # 计算距离是使用distMeas参数给出的距离公式,默认距离函数是distEclud
                distJI = distMeas(centroids[j, :], dataMat[i, :])
                # 如果距离比minDist(最小距离)还小,更新minDist(最小距离)和最小质心的index(索引)
                if distJI < minDist:
                    minDist = distJI
                    minIndex = j
            # 更新簇分配结果为最小质心的index(索引),minDist(最小距离)的平方
            clusterAssment[i, :] = minIndex, minDist ** 2
            iterNum -= 1;
        # print(centroids)
        # 遍历所有质心并更新它们的取值
        for cent in range(k):
            # 通过数据过滤来获得给定簇的所有点
            ptsInClust = dataMat[np.nonzero(clusterAssment[:, 0].A == cent)[0]]
            # 计算所有点的均值,axis=0表示沿矩阵的列方向进行均值计算
            centroids[cent, :] = np.mean(ptsInClust, axis=0)
    # 返回给定迭代次数后误差的值
    return np.mat(clusterAssment[:,1].sum(0))[0,0]

if __name__ == "__main__":
    df=pd.read_csv("./testdata.csv")
    data=df.values
    dataMat=np.matrix(data)

    res=[]
    for i in range(2,20):
        res.append([i,cost(dataMat,i)])

    res=np.matrix(res)

    plt.plot(res[:,0],res[:,1])

    plt.title('Find the best K')
    plt.xlabel('K')
    plt.ylabel('meandistortions')

    plt.show()

KMeans

  最后选取一个较好的聚类结果：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
def kMeans(dataMat, k, distMeas=distEclud, createCent=randCent):
    '''
    创建K个质心,然后将每个点分配到最近的质心,再重新计算质心。
    这个过程重复数次,直到数据点的簇分配结果不再改变为止
    :param dataMat: 数据集
    :param k: 簇的数目
    :param distMeans: 计算距离
    :param createCent: 创建初始质心
    :return:
    '''
    # 获取样本数和特征数
    m, n = np.shape(dataMat)
    # 初始化一个矩阵来存储每个点的簇分配结果
    # clusterAssment包含两个列:一列记录簇索引值,第二列存储误差(误差是指当前点到簇质心的距离,后面会使用该误差来评价聚类的效果)
    clusterAssment = np.mat(np.zeros((m, 2)))
    # 创建质心,随机K个质心
    centroids = createCent(dataMat, k)

    # 初始化标志变量,用于判断迭代是否继续,如果True,则继续迭代
    clusterChanged = True
    while clusterChanged:
        clusterChanged = False
        # 遍历所有数据找到距离每个点最近的质心,
        # 可以通过对每个点遍历所有质心并计算点到每个质心的距离来完成
        for i in range(m):
            minDist = np.inf # 初始化为无穷大
            minIndex = -1
            for j in range(k):
                # 计算数据点到质心的距离
                # 计算距离是使用distMeas参数给出的距离公式,默认距离函数是distEclud
                distJI = distMeas(centroids[j, :], dataMat[i, :])
                # 如果距离比minDist(最小距离)还小,更新minDist(最小距离)和最小质心的index(索引)
                if distJI < minDist:
                    minDist = distJI
                    minIndex = j
            # 如果任一点的簇分配结果发生改变,则更新clusterChanged标志
            if clusterAssment[i, 0] != minIndex: clusterChanged = True
            # 更新簇分配结果为最小质心的index(索引),minDist(最小距离)的平方
            clusterAssment[i, :] = minIndex, minDist ** 2
        # print(centroids)
        # 遍历所有质心并更新它们的取值
        for cent in range(k):
            # 通过数据过滤来获得给定簇的所有点
            ptsInClust = dataMat[np.nonzero(clusterAssment[:, 0].A == cent)[0]]
            # 计算所有点的均值,axis=0表示沿矩阵的列方向进行均值计算
            centroids[cent, :] = np.mean(ptsInClust, axis=0)
    # 返回所有的类质心与点分配结果
    return centroids, clusterAssment

if __name__ == "__main__":
    df=pd.read_csv("./testdata.csv")
    data=df.values
    dataMat=np.matrix(data)
    k=6
    res1,res2=kMeans(dataMat,k)

    for i in range(k):
        x=[]
        y=[]
        for j in range(len(df)):
            if res2[j,0]==i:
                x.append(data[j,0])
                y.append(data[j,1])
        plt.scatter(x, y)

        plt.scatter(res1[i,0],res1[i,1], marker='^',c = 'r',s=300)

    plt.show()

实验结果及数据

  随机生成的数据终究效果不怎么好，最后还是去网上找了两个样例数据来试试（真香）。

数据1

findeBestK

KMeans

数据

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
X,Y
1.658985,4.285136
-3.453687,3.424321
4.838138,-1.151539
-5.379713,-3.362104
0.972564,2.924086
-3.567919,1.531611
0.450614,-3.302219
-3.487105,-1.724432
2.668759,1.594842
-3.156485,3.191137
3.165506,-3.999838
-2.786837,-3.099354
4.208187,2.984927
-2.123337,2.943366
0.704199,-0.479481
-0.392370,-3.963704
2.831667,1.574018
-0.790153,3.343144
2.943496,-3.357075
-3.195883,-2.283926
2.336445,2.875106
-1.786345,2.554248
2.190101,-1.906020
-3.403367,-2.778288
1.778124,3.880832
-1.688346,2.230267
2.592976,-2.054368
-4.007257,-3.207066
2.257734,3.387564
-2.679011,0.785119
0.939512,-4.023563
-3.674424,-2.261084
2.046259,2.735279
-3.189470,1.780269
4.372646,-0.822248
-2.579316,-3.497576
1.889034,5.190400
-0.798747,2.185588
2.836520,-2.658556
-3.837877,-3.253815
2.096701,3.886007
-2.709034,2.923887
3.367037,-3.184789
-2.121479,-4.232586
2.329546,3.179764
-3.284816,3.273099
3.091414,-3.815232
-3.762093,-2.432191
3.542056,2.778832
-1.736822,4.241041
2.127073,-2.983680
-4.323818,-3.938116
3.792121,5.135768
-4.786473,3.358547
2.624081,-3.260715
-4.009299,-2.978115
2.493525,1.963710
-2.513661,2.642162
1.864375,-3.176309
-3.171184,-3.572452
2.894220,2.489128
-2.562539,2.884438
3.491078,-3.947487
-2.565729,-2.012114
3.332948,3.983102
-1.616805,3.573188
2.280615,-2.559444
-2.651229,-3.103198
2.321395,3.154987
-1.685703,2.939697
3.031012,-3.620252
-4.599622,-2.185829
4.196223,1.126677
-2.133863,3.093686
4.668892,-2.562705
-2.793241,-2.149706
2.884105,3.043438
-2.967647,2.848696
4.479332,-1.764772
-4.905566,-2.911070

数据2

数据

findeBestK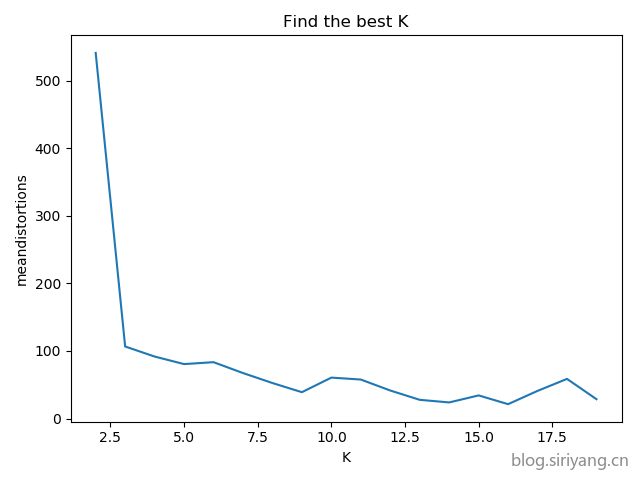

KMeans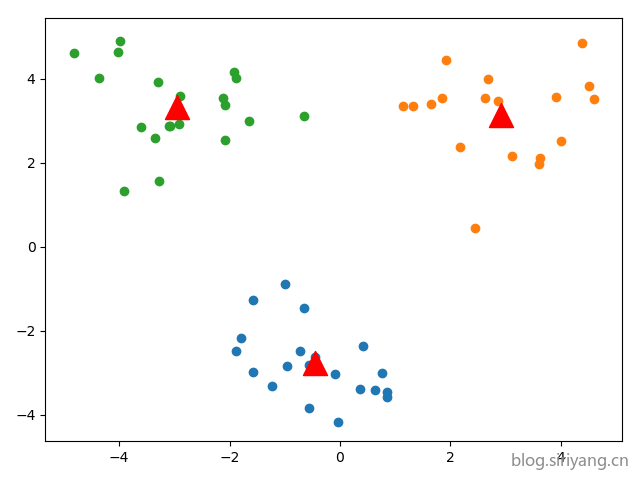

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
3.275154,2.957587
-3.344465,2.603513
0.355083,-3.376585
1.852435,3.547351
-2.078973,2.552013
-0.993756,-0.884433
2.682252,4.007573
-3.087776,2.878713
-1.565978,-1.256985
2.441611,0.444826
-0.659487,3.111284
-0.459601,-2.618005
2.177680,2.387793
-2.920969,2.917485
-0.028814,-4.168078
3.625746,2.119041
-3.912363,1.325108
-0.551694,-2.814223
2.855808,3.483301
-3.594448,2.856651
0.421993,-2.372646
1.650821,3.407572
-2.082902,3.384412
-0.718809,-2.492514
4.513623,3.841029
-4.822011,4.607049
-0.656297,-1.449872
1.919901,4.439368
-3.287749,3.918836
-1.576936,-2.977622
3.598143,1.975970
-3.977329,4.900932
-1.791080,-2.184517
3.914654,3.559303
-1.910108,4.166946
-1.226597,-3.317889
1.148946,3.345138
-2.113864,3.548172
0.845762,-3.589788
2.629062,3.535831
-1.640717,2.990517
-1.881012,-2.485405
4.606999,3.510312
-4.366462,4.023316
0.765015,-3.001270
3.121904,2.173988
-4.025139,4.652310
-0.559558,-3.840539
4.376754,4.863579
-1.874308,4.032237
-0.089337,-3.026809
3.997787,2.518662
-3.082978,2.884822
0.845235,-3.454465
1.327224,3.358778
-2.889949,3.596178
-0.966018,-2.839827
2.960769,3.079555
-3.275518,1.577068
0.639276,-3.412840

2020.2.4更新

0117第一次评测：
代码实现了Kmeans算法，并进行了算法优缺点分析以及对5个数据集的算法测试，采用了手肘法选出了每个数据集的最优K值。

  按照1月17号提交结果的评测来看需要进行算法优缺点分析。

算法分析：
优点：Kmenans算法是最基础的无监督聚类算法，原理简单，实现容易。
缺点：

  1. 收敛较慢
  2. 算法时间复杂度比较高 O(nkt)
  3. 不能发现非凸形状的簇
  4. 需要事先确定超参数K
  5. 对噪声和离群点敏感
  6. 结果不一定是全局最优，只能保证局部最优

结语

  网上KMeans的博客教程非常多，但代码多多少少都有点问题。这个代码算是比较好的了，注释非常详细，但一开始还是有个bug，调了老半天才弄好。就是在求欧式距离那个函数里，原来使用的求和函数是sum，但是用这个求和函数计算numpy矩阵算不出来，导致后面一直报错，最后换成numpy.sum就OK了。
  还有一个问题就是原作者一开始使用的是手动读取分割文本数据，我直接调用的pandas函数，导致读进来的数据格式有点不一样，也跑不成。后来调试发现他把数据都转成了numpy矩阵，而我用的是list矩阵，之后手动转换一下就解决了。
  感觉做机器学习这些最麻烦的就是数据格式的处理，尤其是不能把numpy和list随便混用，不然后面多半要翻车。不过随着不断练习，数据处理经验逐渐丰富，越往后做起来会更得心应手一些。

-------- 本文结束 感谢阅读 --------
相关文章
觉得文章写的不错的话，请我喝瓶怡宝吧！😀
  • 本文标题： X-Data数据工程基础实践（三）
  • 本文作者： SiriYang
  • 创建时间： 2020年01月09日 - 15时01分
  • 修改时间： 2021年10月29日 - 18时10分
  • 本文链接： https://blog.siriyang.cn/posts/20200109153247id.html
  • 版权声明： 本博客所有文章除特别声明外，均采用 CC BY-NC-SA 4.0 许可协议。转载请注明出处！
0%