高数
极限与连续
无穷小性质
- $$ x\sim \sin x \sim \tan x \sim \arcsin x \sim \arctan x \sim e^x-1 \sim \ln (1+x) $$
- $$
\begin{cases}
1-\cos x \sim \frac{1}{2} x^2 \[2ex]
1-\cos ^a x \sim \frac{a}{2} x^2
\end{cases}
$$ - $$(1+\Delta )^a-1 \sim a\Delta (\Delta \to 0) $$
- $$a^x-1 \sim x\ln a $$
- $$e^x-1 \sim x $$
重要极限
- $$ \lim_{\Delta \to 0 }\frac{\sin \Delta}{\Delta}=1 $$
- $$ \lim_{\Delta \to 0 }(1+\Delta)^{\frac{1}{\Delta}}=e $$
- $$ \lim_{\Delta \to +\infty }x^\frac{1}{x}=1 ,\quad (\infty^0) $$
- $$ \lim_{\Delta \to 0^+ }x^x=1 ,\quad (0^0) $$
- $$ \lim_{x \to 0^+ }x\ln x=0 $$
- $$ \lim_{x \to 0^+ }x^a\ln x=0 ,\quad (a>0) $$
其他
当 $X\to x_0$ 时，若 $f(x)\to 0$ ，$g(x)\to 0$ 则 $e^{f(x)}-e^{g(x)} \sim f(x)-g(x)$。
微分学
求导公式
- $$ (c)’=0 $$
- $$ (x^a)’=ax^{a-1} $$
- $$ (a^x)’=a^x \ln a ,\quad (e^x)’=e^x $$
- $$ (\log_a x)’=\frac{1}{x\ln a} ,\quad (\ln x)’=\frac{1}{x} $$
- $$ (\sin x)’=\cos x $$
- $$ (\cos x)’=-\sin x $$
- $$ (\tan x)’=\sec^2 x $$
- $$ (\cot x)’=-\csc^2 x $$
- $$ (\sec x)’=\sec x \tan x $$
- $$ (\csc x)’=-\csc x \cot x $$
- $$ (\arcsin x)’=\frac{1}{\sqrt{1-x^2}} $$
- $$ (\arccos x)’=-\frac{1}{\sqrt{1-x^2}} $$
- $$ (\arctan x)’=\frac{1}{1+x^2} $$
- $$ (arccot x)’=-\frac{1}{1+x^2} $$
- 几个初等函数的 $n$ 阶导数公式
- $$(a^x)^{(n)}=a^x(\ln a)^n$$
- $$(e^x)^{(n)}=e^x$$
- $$(\sin kx)^{(n)}=k^n\sin (kx+n\cdot \frac{\pi}{2})$$
- $$(\cos kx)^{(n)}=k^n\cos (kx+n\cdot \frac{\pi}{2})$$
- $$(\ln x)^{(n)}=(-1)^{n-1}\frac{(n-1)!}{x^n}(x>0)$$
- $$[\ln (1+x)]^{(n)}=(-1)^{n-1}\frac{(n-1)!}{(1+x)^n}(x>-1)$$
- $$[(x+x_0)^m]^{(n)}=m(m-1)(m-2)\dots (m-n+1)(x+x_0)^{m-n}$$
- $$ (\frac{1}{ax+b})^{(n)}=\frac{(-1)^n n! a^n}{(ax+b)^{n+1}} $$
- $$ (UV)^{(n)}=\mathrm{C}^0_n U^{(n)}V+\mathrm{C}^1_n U^{(n-1)}V’+\dots+\mathrm{C}^n_n UV^{(n)} $$
定理证明中值定理
涉及函数 $f(x)$ 的中值定理
设 $f(x)$ 在 $[a,b]$ 上连续，则
定理1 （有界与最值定理）
$m \le f(x) \le M$ ,其中， $m,M$ 分别为 $f(x)$ 在 $[a,b]$ 上的最小值与最大值
定理2 （介值定理）
当 $m \le \mu \le M$ 时，存在 $\xi \in [a,b]$ ,使得 $f(\xi )=\mu$
定理3 （平均值定理）
当 $a<x_1<x_2<\dots <x_n<b$ 时，在 $[x_1,x_2]$ 内至少存在一点 $\xi$ ，使
$$f(\xi )=\frac{f(x_1)+f(x_2)+\dots +f(x_n)}{n}$$
定理4 （零点定理）
当 $f(a)\cdot f(b)<0$ 时，存在 $\xi \in (a,b)$ ，使得 $f(\xi )=0$
涉及导数（微分）的中值定理
定理5 （费马定理）
设 $f(x)$ 满足在 $x_0$ 点处（1）可导；（2）取极值，则 $f’(x_0)=0$
定理6 （罗尔定理）
设 $f(x)$ 满足（1）$[a,b]$ 上连续；（2）$(a,b)$ 内可导；（3）$f(a)=f(b)$ ，则存在 $\xi \in (a,b)$ ，使得 $f’(\xi )=0$
定理7 （拉格朗日中值定理）
设 $f(x)$ 满足（1）$[a,b]$ 上连续；（2）$(a,b)$ 内可导 ，则存在 $\xi \in (a,b)$ ，使得 $f(b)-f(a)=f’(\xi )(b-a)$ ，或写成 $f’(\xi )=\frac{f(b)-f(a)}{b-a}$
定理8 （柯西中值定理）
设 $f(x)，g(x)$ 满足（1）$[a,b]$ 上连续；（2）$(a,b)$ 内可导；（3）$g’(x)\ne 0$ ，则存在 $\xi \in (a,b)$ ，使得 $\frac{f(b)-f(a)}{g(b)-g(a)}=\frac{f’(\xi )}{g’(\xi )}$
涉及积分的中值定理
定理9 （积分中值定理）
设 $f(x)$ 在$[a,b]$ 上连续 ，则存在 $\xi \in [a,b]$ ，使得 $\int_{a}^{b}f(x)dx=f(\xi )(b-a)$
中值定理辅助函数
- $ f’(\xi)+kf(\xi)=0 $
$$ \varphi(x)=e^{kx}f(x) $$ - $ f’(\xi)+kf(\xi)=s $
$$ \varphi(x)=e^{kx}[f(x)-\frac{s}{k}] $$ - $\xi f’(\xi)+kf(\xi)=0$
$$ \varphi(x)=x^{k}f(x) $$ - $f’’(x)-f(x)=0$
$$\varphi (x)=e^x[f’(x)-f(x)]$$
泰勒公式
泰勒公式
常规
$$ f(x)=f(x_0)+f’(x_0)(x-x_0)+\frac{f’’(x_0)}{2!} (x-x_0)^2 + \dots + \frac{f^n(x_0)}{n!} (x-x_0)^n $$
麦克劳林
- $$ e^x=1+x+\frac{x^2}{2!}+\dots+\frac{x^n}{n!}+o(x^n) $$
- $$ \ln (1+x) =x-\frac{x^2}{2}+\frac{x^3}{3}-\dots+\frac{(-1)^{n-1}}{n}x^n+o(x^n) $$
- $$ \arctan x =x-\frac{x^3}{3}+\frac{x^5}{5}-\frac{x^7}{7}\dots $$
- $$ \sin x=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\dots+\frac{(-1)^n}{(2n+1)!}x^{2n+1}+o(x^{2n+1}) $$
- $$ \cos x=1-\frac{x^2}{2!}+\frac{x^4}{4!}-\dots+\frac{(-1)^n}{(2n)!}x^{2n}+o(x^{2n}) $$
- $$ \frac{1}{1-x} =1+x+x^2+\dots+x^n+o(x^n) $$
- $$ \frac{1}{1+x} =1-x+x^2-x^3+\dots+(-1)^n x^n+o(x^n) $$
- $$ (1+x)^a =1+ax+\frac{a(a-1)}{2!}x^2+\frac{a(a-1)(a-2)}{3!}x^3+\dots $$
不规则
- $$ \arcsin x=x+\frac{x^3}{3!}+o(x^3) $$
- $$ \tan x=x+\frac{x^3}{3}+o(x^3)$$
反函数求导
$y=f(x) \Rightarrow x=\varphi (y):$
- $$ \varphi’(y)= \frac{1}{f’(x)} $$
- $$ \varphi’’(y)= -\frac{f’’(x)}{f’^3(x)} $$
其他
设$f(x)$在$X=X_0$处可导，$g(x)$在$X=X_0$处连续但不可导，则$F(x)=f(x)\cdot g(x)$在$x=x_0$处可导当且仅当$f(x_0)=0$。
判别极值的第三充分条件
设 $f(x)$ 在 $x_0$ 处 $n$ 阶可导，且 $f^{(m)}(x_0)=0(m=1,2,\dots ,n-1),f^{(n)}(x_0)\ne 0(n \ge 2)$，则
- 当 $n$ 为偶数且 $f^{(n)}(x_0) < 0$ 时 $f(x)$ 在 $x_0$ 处取得极大值
- 当 $n$ 为偶数且 $f^{(n)}(x_0) > 0$ 时 $f(x)$ 在 $x_0$ 处取得极小值
判别拐点的第三充分条件
设 $f(x)$ 在 $x_0$ 处 $n$ 阶可导 $f^{(m)}(x_0)=0(m=2,\dots ,n-1)$,$f^{(n)}(x_0)\ne 0(n \ge 3)$ ，则当 $n$ 为奇数时， $(x_0,f(x_0))$ 为拐点
多元微分
多元微分
无条件极值
$z=f(x,y)[或F(x,y,z)=0] \quad x,y\in D(开)$
1.
$$
\begin{cases}
\frac{\partial z}{\partial x}=0 \
\frac{\partial z}{\partial y}=0
\end{cases}
\to
\begin{cases}
x=x_0 \
y=y_0
\end{cases}
$$
$(x,y)=(x_0,y_0)$
$A=f_{xx}’’(x_0,y_0),B=f_{xy}’’(x_0,y_0),C=f_{yy}’’(x_0,y_0)$
$$AC-B^2
\begin{cases}
0 , & \surd \quad \begin{cases}
A>0 , & 小 \
A<0 , & 大
\end{cases}\
<0 ,& \times
\end{cases}
$$
多元可微定义
$$\lim_{\rho \to 0}\frac{F(x,y)-F_x’(x,y)x-F_y’(x,y)y}{\rho}=0 , \quad \rho=\sqrt{x^2+y^2}$$
积分学
基本性质
f(x)是连续的奇函数，则其所有原函数都是偶函数。
f(x)是连续的偶函数，则其所有原函数中只有一个是奇函数。积分公式
- $$ \int k dx = kx + C $$
- $$
\int x^a dx =
\begin{cases}
\frac{1}{a+1}x^{a+1}+C, & a \ne -1 \[2ex]
\ln |x|+C, & a=-1
\end{cases}
$$ - $$
\int a^x dx =
\begin{cases}
\frac{a^x}{\ln a}+C, & a \ne e \[2ex]
e^x+C, & a = e
\end{cases}
$$ - $$ \int \sin x dx=-\cos x + C $$
- $$ \int \cos x dx=\sin x + C $$
- $$ \int \tan x dx=-\ln |\cos x| + C $$
- $$ \int \cot x dx=\ln |\sin x| + C $$
- $$ \int \sec x dx=\ln |\sec x + \tan x| + C $$
- $$ \int \csc x dx=\ln |\csc x - \cot x| + C $$
- $$ \int \sec^2 x dx=\tan x + C $$
- $$ \int \csc^2 x dx=-\cot x + C $$
- $$ \int \sec x\tan x dx=\sec x + C $$
- $$ \int \csc x\cot x dx=-\csc x + C $$
- 平方和、平方差
- $$ \int \frac{1}{\sqrt{1-x^2}} dx=\arcsin x + C $$
- $$ \int \frac{1}{\sqrt{a^2-x^2}} dx=\arcsin \frac{x}{a} + C $$
- $$ \int \frac{1}{\sqrt{x^2+a^2}} dx=\ln(x+\sqrt{x^2+a^2}) + C $$
- $$ \int \frac{1}{\sqrt{x^2-a^2}} dx=\ln \left|x+\sqrt{x^2-a^2} \right| + C $$
- $$ \int \frac{1}{1+x^2} dx=\arctan x + C $$
- $$ \int \frac{1}{a^2+x^2} dx=\frac{1}{a} \arctan \frac{x}{a} + C $$
- $$ \int \frac{1}{x^2-a^2} dx=\frac{1}{2a} \ln \bigg|\frac{x-a}{x+a}\bigg| + C $$
- $$ \int \sqrt{x^2+a^2} dx=\frac{x}{2}\sqrt{x^2+a^2} + \frac{a^2}{2}\ln (x+\sqrt{x^2+a^2}) + C $$
- $$ \int \sqrt{x^2-a^2} dx=\frac{x}{2}\sqrt{x^2-a^2} - \frac{a^2}{2}\ln \left|x+\sqrt{x^2-a^2}\right| + C $$
- $$ \int \sqrt{a^2-x^2} dx=\frac{x}{2} \sqrt{a^2-x^2}+\frac{a^2}{2}\arcsin \frac{x}{a} + C $$
其他
以下公式为平时刷题所总结，记住可加快解题速度。
- $$ \int xe^x dx=(x-1)e^x + C $$
- $$\int \ln x dx=x(\ln x-1)+C$$
- $$\int x^a\ln x dx=\frac{1}{a+1}x^{a+1}(\ln x-\frac{1}{a+1})+C$$
- $$ \int \sin 2x dx=\sin^2 x + C $$
- $$\int x\sin x dx= \sin x - x\cos x+C$$
- $$\int x\cos x dx=x\sin x+ \cos x+C$$
- $$\int \frac{\cos x-\sin x}{\sin x+\cos x} dx=\ln (\sin x+\cos x)+C$$
- $$\int_0^{\frac{\pi}{2}} f(\sin x) dx=\int_0^{\frac{\pi}{2}} f(\cos x) dx$$
- $$\int_0^{\pi} xf(\sin x) dx=\frac{\pi}{2} \int_0^{\pi} f(\sin x) dx=\pi \int_0^{\frac{\pi}{2}} f(\sin x) dx$$
- $$\int_0^{2\pi} f(|\sin x|) dx=4 \int_0^{\frac{\pi}{2}} f(\sin x) dx $$
- 若$f(x)$在$[0,1]$上有一阶连续导函数，则 $$\lim_{n\to \infty}\int_0^1 f(x)\sin nxdx=0$$
有理函数积分
分解的基本原则
- $Q_m(x)$ 的一次因式 $(ax+b)$ 产生一项 $$\frac{A}{ax+b}$$
- $Q_m(x)$ 的 $k$ 重因式 $(ax+b)^k$ 产生 $k$ 项，分别为 $$\frac{A_1}{ax+b}+\frac{A_2}{(ax+b)^2}+\dots + \frac{A_k}{(ax+b)^k}$$
- $Q_m(x)$ 的二次单因式 $px^2+ax+r$ 产生一项 $$\frac{Ax+B}{px^2+ax+r}$$
- $Q_m(x)$ 的 $k$ 重二次因式 $(px^2+q+r)^k$ 产生 $k$ 项 $$\frac{A_1x+B_1}{px^2+ax+r}+\frac{A_2x+B_2}{(px^2+ax+r)^2}+\dots +\frac{A_kx+B_k}{(px^2+ax+r)^k}$$
$\Gamma$ 函数
$\Gamma$ 函数的定义为：
$$\Gamma (a)=\int_0^{+\infty} x^{a-1}e^{-x} dx$$
$\Gamma$ 函数的性质为：
$$\Gamma (a+1)=a\Gamma (a);\quad \Gamma(n+1)=n!;\quad \Gamma(\frac{1}{2})=\sqrt{\pi}$$
反常积分判别法
无限区间
$$\lim_{x \to +\infty}x^\alpha \cdot f(x)=k(\ne \infty)\begin{cases} 收敛, & \alpha >1 \ 发散 , & \alpha \le 1 \end{cases}$$
区间有限
$$\lim_{x \to a}(x-a)^\alpha \cdot f(x)=k(\ne \infty)\begin{cases} 收敛, & \alpha <1 \ 发散 , & \alpha \ge 1 \end{cases}$$
二重积分对称性
若$Ｄ$关于$y$轴对称，且位于$y$轴右侧区域为$D_1$，有
$$若f(-x,y)=-f(x,y),则\iint_D f(x,y)dxdy=0$$
$$若f(-x,y)=f(x,y),则\iint_D f(x,y)dxdy=2\iint_{D_1}f(x,y)dxdy$$
若$Ｄ$关于$x$轴对称，且位于$x$轴上侧区域为$D_1$，有
$$若f(x,y)=-f(x,y),则\iint_D f(x,y)dxdy=0$$
$$若f(x,y)=f(x,y),则\iint_D f(x,y)dxdy=2\iint_{D_1}f(x,y)dxdy$$
若$Ｄ$关于$y=x$轴对称，则
$$\iint_D f(x,y)dxdy=\iint_D f(y,x)dxdy$$
微分方程
一阶齐次线性微分方程
$\frac{dy}{dx}+P(x)y=0$：
$$ y=Ce^{-\int P(x)dx } ,\quad C为任意常数 $$
一阶非齐次线性微分方程
$\frac{dy}{dx}+P(x)y=Q(x)$：
$$ y=\left[ \int Q(x)e^{\int P(x)dx }dx + C \right]e^{-\int P(x)dx} $$
解的性质
n阶齐次线性微分方程：
$ y^{(n)}+a_1(x)y^{(n-1)}+\dots +a_{n-1}(x)y’+a_n(x)y=0 \quad (\ast) $
n阶非齐次线性微分方程：
$ y^{(n)}+a_1(x)y^{(n-1)}+\dots +a_{n-1}(x)y’+a_n(x)y=f(x) \quad (\ast \ast) $
1、$ \varphi_1(x) , \dots ,\varphi_s(x) 为（\ast）解 $
$则 k_1 \varphi_1(x) + \dots +k_s \varphi_s(x) 为（\ast）解$
2、$ \varphi_1(x) , \dots ,\varphi_s(x) 为（\ast \ast）解 $
$(1)\quad k_1 \varphi_1(x) + \dots +k_s \varphi_s(x) 为（\ast）解 \Longleftrightarrow k_1+\dots +k_s=0 $
$(2)\quad k_1 \varphi_1(x) + \dots +k_s \varphi_s(x) 为（\ast \ast）解 \Longleftrightarrow k_1+\dots +k_s=1 $
物理几何应用
一元函数微分学的物理应用
- $$v=\lim_{\Delta t \to 0}\frac{\Delta s}{\Delta t}=s’(t)$$
- $$a(t)=\lim_{\Delta t \to 0}\frac{\Delta v}{\Delta t}=v’(t)=s’’(t)$$
一元函数微分学的几何应用
斜率、法线
两条正交的直线斜率之积为-1。
曲率
$$ K=\frac{|y’’|}{(1+y’^2)^{3/2}} $$
曲率半径
$$ R=\frac{1}{K} $$
斜渐近线公式
若
$$\lim_{x \to + \infty} \frac{f(x)}{x}=\lim_{x \to -\infty} \frac{f(x)}{x}=k$$
$$\lim_{x \to +\infty}[f(x)-kx]=\lim_{x \to -\infty}[f(x)-kx]=b$$
则 $y=kx+b$ 是曲线 $y=f(x)$ 的一条斜渐近线
一元函数积分学的几何应用
$f(x)$在$[a,b]$上的均值：
$$\bar f=\frac{\int_a^b f(x) dx}{\int_a^b dx}$$
平面曲线的弧长
- 若平面光滑曲线 $L$ 由 $y=y(x)(a\le x \le b)$ 给出，则 $$L=\int_a^b \sqrt{1+[y’(x)]^2}dx$$
- 若平面光滑曲线 $L$ 由参数式 $\begin{cases} x=x(t) \ y=y(t) \end{cases},(\alpha\le t \le \beta)$ 给出，则 $$L=\int_{\alpha}^{\beta} \sqrt{[x’(t)]^2+[y’(t)]^2}dt$$
- 若平面光滑曲线 $L$ 由 $r=r(\theta)(\alpha \le \theta \le \beta)$ 给出，则 $$L=\int_{\alpha}^{\beta} \sqrt{[r(\theta)]^2+[r’(\theta)]^2}d\theta$$
面积
- 设 $D$ 由 $y=f(x)\ge 0,x=a$ 及 $x=b(a<b)$ 围成，则 $D$ 的面积为 $A=\int_a^b f(x)dx$
- 设 $D$ 由曲线 $y=f(x),y=g(x),x=a$ 及 $x=b(a<b)$ 围成，则 $D$ 的面积为 $$A=\int_a^b |f(x)-g(x)|dx$$
- 设 $D$ 由 $r=r(\theta)(\alpha\le \theta \le \beta)$ 围成,用元素法求 $D$ 的面积如下：取 $d\theta \subset [\alpha,\beta]$ ，则 $dA=\frac{1}{2} r^2(\theta)d\theta$ ，于是 $D$ 的面积为 $A=\frac{1}{2}\int_{\alpha}^{\beta} r^2(\theta)d\theta$
- 设 $D$ 由 $r=r_1(\theta),r=r_2(\theta)(r_1(\theta)\le r_2(\theta),\alpha \le \theta \le \beta)$ 围成，则 $D$ 的面积为 $$A=\frac{1}{2}\int_{\alpha}^{\beta} [r_2^2(\theta)-r_1^2(\theta)]d\theta$$
旋转曲面的面积
- 曲线 $y=y(x)$ 在区间 $[a,b]$ 上的曲线弧段绕 $x$ 轴旋转一周所得到的旋转曲面的面积 $$S=2\pi \int_a^b |y(x)|\sqrt{1+[y’(x)]^2}dx$$
- 曲线 $x=x(t),y=y(t)(\alpha \le t \le \beta,x’(t)\ne 0)$ 在区间 $[\alpha,\beta]$ 上的曲线弧段绕 $x$ 轴旋转一周所得到的旋转曲面的面积 $$S=2\pi \int_a^b |y(t)|\sqrt{[x’(t)]^2+[y’(t)]^2}dt$$
平行截面面积为已知的立体体积
在区间 $[a,b]$ 上，垂直于 $x$ 轴的平面截立体 $\Omega$ 所得到的截面面积为 $x$ 的连续函数 $A(x)$ ，则 $\Omega$ 的体积为 $$V=\int_a^bA(x)dx$$
微分方程物理应用
$$v=\frac{dx}{dt}$$
$$a=\frac{dv}{dt}=\frac{d^2x}{dt^2}=v\frac{dv}{dx}$$
常用几何体
椭圆
- 公式 $$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$$
- 面积 $$S=\pi ab$$
球体
- 表面积 $$S=4\pi r^2$$
- 体积 $$V=\frac{4}{3}\pi r^3$$
几种常用曲线
1.星型线
$$x^{\frac{2}{3}}+y^{\frac{2}{3}}=a^{\frac{2}{3}}$$
$$
\begin{cases}
x=a\cos ^3 \theta \
y=a\sin ^3 \theta
\end{cases}
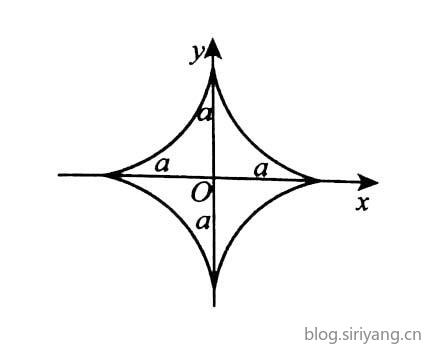
$$
2.摆线
$$
\begin{cases}
x=a(\theta-\sin \theta) \
y=a(1-\cos \theta)
\end{cases}
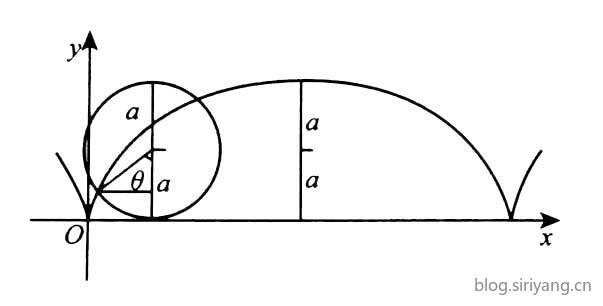
$$
对$0\le \theta \le 2\pi$区域进行二重积分$\iint_D f(x,y) dxdy$:
$D={x,y | 0\le x \le 2\pi , 0\le y \le g(x) }$
$\iint_D f(x,y) dxdy=\int_0^{2\pi} dx \int_0^{g(x)} f(x,y) dy $
消掉$y$以后，将$x=a(\theta-\cos\theta);y=g(x)=a(1-\sin\theta)$带入当成参数方程求解即可。
3.心型线
$$x^2+y^2+ax=a\sqrt{x^2+y^2}$$
$$r =a(1-\cos \theta)$$
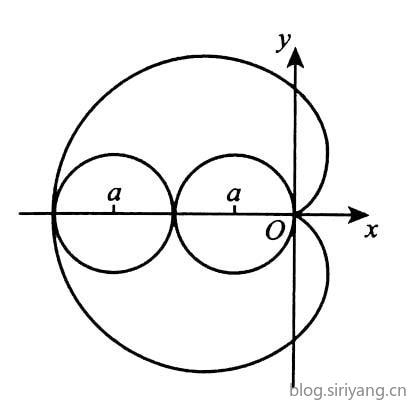
$x=r\cos \theta = r(\theta)\cos \theta$
$y=r\sin \theta = r(\theta)\sin \theta$
4.双扭线
$$(x^2+y^2)^2=a^2(x^2-y^2)$$
$$r ^2=a^2 \cos 2\theta$$
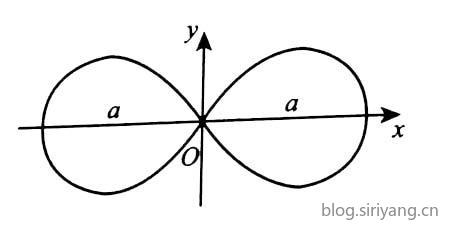
常用物理公式
牛顿第二定律
$$f=ma$$
水压
$$P=\rho g h$$
万有引力公式
$$F=G \frac{M_1 \times M_2}{r^2}$$
多元积分几何应用
形心
$$\bar x=\frac{\iint_{D} x dxdy }{\iint_{D} dxdy}$$
$$\bar y=\frac{\iint_{D} y dxdy }{\iint_{D} dxdy}$$
质心
密度：$\rho(x,y)$
$$\bar x=\frac{\iint_{D} x \rho(x,y) dxdy }{\iint_{D} \rho(x,y) dxdy}$$
$$\bar y=\frac{\iint_{D} y \rho(x,y) dxdy }{\iint_{D} \rho(x,y) dxdy}$$
常用基础公式
数列基础
（1） 等差数列 首相为 $ a_1 $ ，公差为 $d(d\ne 0)$ 的数列 $a_1,a_1+d,a_1+2d,\dots ,a_1+(n-1)d,\dots$
1. 通项公式 $$a_n =a_1 +(n-1)d$$
2. 前 $n$ 项和 $$S_n=\frac{n}{2}[2a_1 +(n-1)d]=\frac{n}{2}(a_1+a_n)$$
（2）等比数列 首项为 $a_1$ 公比为 $r(r\ne 0)$ 的数列 $a_1,a_1r,a_1r^2,\dots ,a_1r^{n-1},\dots$
1. 通项公式 $$a_n=a_1r^{n-1}$$
2. 前 $n$ 项和 $$S_n=\frac{a_1 (1-r^n)}{1-r}(r\ne 1)$$
$$常用 1+r+r^2+\dots +r^{n-1}=\frac{1-r^n}{1-r}$$
（3）一些数列前 $n$ 项的和：
- $$\sum^{n}_{k=1}k=1+2+3+\dots +n=\frac{n(n+1)}{2}$$
- $$\sum^{n}_{k=1}k^2=1^2+2^2+3^2+\dots +n^2=\frac{n(n+1)(2n+1)}{6}$$
- $$\sum^{n}_{k=1}k^3=1^3+2^3+3^3+\dots +n^3= \bigg[ \frac{n(n+1)}{2} \bigg] ^2 $$
- $$\sum^{n}_{k=1}(2k-1)=1+3+5+\dots +(2n-1)=n^2$$
- $$\sum^{n}_{k=1}k(k+1)=1 \times 2 + 2 \times 3+ 3 \times 4+ \dots +n(n+1)=\frac{n(n+1)(n+2)}{3}$$
- $$\sum^{n}_{k=1}\frac{1}{k(k+1)}=\frac{1}{1 \times 2}+\frac{1}{2 \times 3}+\frac{1}{3 \times 4}+ \dots +\frac{1}{n(n+1)}=\frac{n}{n+1}$$
三角函数基础
三角函数基本关系
$$ \sin a \cdot \csc a=1, \quad \csc a=\frac{1}{\sin a}, \quad \cos a \cdot \sec a=1, \quad \sec a=\frac{1}{\cos a} $$
$$ \tan a \cdot \cot a=1, \quad \cot a =\frac{1}{\tan a}, \quad \tan a =\frac{\sin a}{\cos a}, \quad \cot a=\frac{\cos a}{\sin a}$$
$$ \sin ^2 a + \cos ^2 a=1, \quad 1-\sin ^2 a=\cos ^2 a, \quad 1-\cos ^2 a= \sin ^2 a$$
$$ \sec ^2 a - \tan ^2 a=1, \quad 1+\tan ^2 a=\sec ^2 a, \quad \sec ^2 a- 1= \tan ^2 a$$
$$ \csc ^2 a - \cot ^2 a=1, \quad 1+\cot ^2 a=\csc ^2 a, \quad \csc ^2 a-1= \cot ^2 a$$
重要公式
倍角公式
$$\sin 2a=2\sin a \cos a ,\quad \cos 2a=\cos ^2a - \sin ^2a=1-2\sin ^2a=2\cos ^2a-1 $$
$$\sin 3a=-4\sin ^3a+3\sin a, \quad \cos 3a=4\cos ^3a-3\cos a$$
$$\sin ^2a=\frac{1}{2}(1-\cos 2a), \quad \cos^2 a=\frac{1}{2}(1+\cos 2a) \quad (降幂公式)$$
$$\tan 2a=\frac{2\tan a}{1-\tan ^2a}, \quad \cot 2a=\frac{\cot ^2a-1}{2\cot a}$$
半角公式
$$\sin ^2\frac{a}{2}=\frac{1}{2}(1-\cos a),\quad \cos ^2\frac{a}{2}=\frac{1}{2}(1+\cos a) \quad (降幂公式) $$
$$\sin \frac{a}{2}=\pm \sqrt{\frac{1-\cos a}{2}}, \quad \cos \frac{a}{2}=\pm \sqrt{\frac{1+\cos a}{2}}$$
$$\tan \frac{a}{2}=\frac{1-\cos a}{\sin a}=\frac{\sin a}{1+\cos a}=\pm \sqrt{\frac{1-\cos a}{1+\cos a}}$$
$$\cot \frac{a}{2}=\frac{\sin a}{1-\cos a}=\frac{1+\cos a}{\sin a}=\pm \sqrt{\frac{1+\cos a}{1-\cos a}}$$
和差公式
$$\sin (a\pm b)=\sin a \cos b \pm \cos a \sin b, \quad \cos (a\pm b)=\cos a \cos b \mp \sin a \sin b$$
$$\sin x+\cos x=\sqrt{2}\sin (x+\frac{\pi}{4}) ,\quad \sin x-\cos x=-\sqrt{2}\cos (x+\frac{\pi}{4})$$
$$\tan (a\pm b)=\frac{\tan a \pm \tan b}{1 \mp \tan a \tan }, \quad \cot(a \pm b)=\frac{\cot a \cot b \mp 1}{\cot b \pm \cot a}$$
积化和差与和差化积公式
（1）积化和差公式
$$\sin a\cos b =\frac{1}{2}[\sin (a+b)+\sin (a-b)],\quad \cos a \sin b=\frac{1}{2}[\sin (a+b)-\sin (a-b)]$$
$$\cos a\cos b=\frac{1}{2}[\cos (a+b)+\cos (a-b)],\quad \sin a\sin b=\frac{1}{2}[\cos (a-b)-\cos (a+b)]$$
（2）和差化积公式
$$\sin a+\sin b=2\sin \frac{a+b}{2} \cos \frac{a-b}{2},\quad \sin a-\sin b=2\sin \frac{a-b}{2} \cos \frac{a+b}{2}$$
$$\cos a+\cos b=2\cos \frac{a+b}{2} \cos \frac{a-b}{2},\quad \cos a-\cos b=-2\sin \frac{a+b}{2} \sin \frac{a-b}{2}$$
万能公式
$$若u=\tan \frac{x}{2} (-\pi < x < \pi),则 \sin x= \frac{2u}{1+u^2},\cos x=\frac{1-u^2}{1+u^2}$$
经典不等式
- 设 $a,b$ 为实数，则
- $$2|ab| \le a^2+b^2$$
- $$|a \pm b| \le |a| + |b|$$
- $$||a|-|b|| \le |a-b|$$
- 离散情况：设 $a_1,a_2,\dots ,a_n$ 为实数，则 $$|a_1\pm a_2\pm \dots \pm a_n| \le |a_1| + |a_2| + \dots + |a_n|$$
- 连续情况：设 $f(x)$ 在 $[a,b]$ 上可积，则 $$\left|\int_{a}^{b} f(x)dx \right| \le \int_{a}^{b}|f(x)|dx(a<b)$$
- 设 $a_1,a_2,\dots ,a_n$ ，则
- $$\frac{a_1+a_2+\dots +a_n}{n} \ge \sqrt[n]{a_1a_2\dots a_n}(当且仅当 a_1=a_2=\dots =a_n 时等号成立)$$
- $$\left|\frac{a_1+a_2+\dots +a_n}{n}\right| \le \sqrt{\frac{a_1^2+a_2^2+\dots +a_n^2}{n}}$$
- 当 $n=2$ 时,$$\sqrt{ab}\le \frac{a+b}{2} \le \sqrt{\frac{a^2+b^2}{2}}(a,b>0)$$
- 当 $n=3$ 时,$$\sqrt[3]{abc}\le \frac{a+b+c}{3} \le \sqrt{\frac{a^2+b^2+c^2}{3}}(a,b,c>0)$$
- 推广：设 $b_i \ge 0 (i=1,2,\dots ,k),m_1,\dots ,m_k$ 是正整数，则 $$\frac{m_1b_1+\dots +m_k+b_k}{m_1+\dots +m_k} \ge (b_1^{m_1}\dots b_k^{m_k})^{\frac{1}{m_1+\dots +m_k}}$$
- 设 $x>0,y>0,p>0,q>0,\frac{1}{p}+\frac{1}{q}=1$ ,则 $$xy \le \frac{x^p}{p}+\frac{y^q}{q}$$
- $$(a^2+b^2)(c^2+d^2)\ge (ac+bd)^2$$
- 推广 $$(a_1b_1 + a_2b_2 +a_3b_3)\le (a_1^2+a_2^2+a_3^2)(b_1^2+b_2^2+b_3^2)$$
- 若 $f(x),g(x)$ 在 $[a,b]$ 上可积且平方可积，则 $$\left[\int_a^b f(x)\cdot g(x)dx\right]^2 \le \int_a^b f^2(x)dx\cdot \int_a^b g^2(x)dx$$
- 设 $f(x)$ 在 $[a,b]$ 上 $p$ 次方可积，$g(x)$ 在 $[a,b]$ 上 $q$ 次方可积，则 $$\left|\int_a^b f(x)\cdot g(x)dx\right| \le \left[\int_a^b |f(x)|^p dx\right]^{\frac{1}{p}}\cdot \left[\int_a^b |g(x)|^q dx\right]^{\frac{1}{q}},其中，p>1,\frac{1}{p}+\frac{1}{q}=1$$
- 其他重要不等式
- 设 $a>b>0$ ，则 $$\begin{cases} 当 n>0 时,a^n>b^n \ 当 n<0 时,a^n<b^n \end{cases}$$
- 若 $0<a<x<b,0<c<y<d$ ，则 $$\frac{c}{b}<\frac{y}{x}<\frac{d}{a}$$
- $$\sin x<x<\tan x(0<x<\frac{\pi}{2}),\quad \sin x<x(x>0)$$
- $$\arctan x\le x \le \arcsin x(0\le x \le 1)$$
- $$e^x \ge x+1 (\forall x),\quad x-1 \ge \ln x(x>0)$$
- $$\frac{1}{1+x}<\ln (1+\frac{1}{x})<\frac{1}{x}(x>0)$$
- 若 $\lim_{n \to \infty}u_n=0$ 则 ${u_n}$ 有界，即存在 $M>0$ ，使得 $|u_n|\le M$
- 闭区间上连续函数必有界，即设 $f(x)$ 在 $[a,b]$ 上连续，则存在 $M>0$ ，使得 $|f(x)|\le M$
- 闭区间上连续函数必有最大值和最小值，即设 $f(x)$ 在 $[a,b]$ 上连续，则 $m\le f(x) \le M $ ，其中 $m,M$ 分别为 $f(x)$ 在 $[a,b]$ 上的最小值与最大值
- 若函数 $f(x)$ 在区间 $[a,b]$ 上单调增加且可导，且 $f’(x)\ge 0$ ，则 $f(a)\le f(x) \le f(b)$
- 若函数 $f(x)$ 在区间 $[a,b]$ 的图像时凹的，且二阶可导，则 $f’’(x)\ge 0$
- 设 $f(x)\le g(x),x\in [a,b]$ ，则 $$\int_a^b f(x)dx \le \int_a^b g(x)dx$$
其他重要结论
指数运算法则
$$a^\alpha\cdot a^\beta =a^{\alpha + \beta}, \quad \frac{a^\alpha}{a^\beta}=a^{\alpha - \beta}, \quad (a^\alpha)^\beta=a^{\alpha \beta}, \quad (ab)^\alpha=a^\alpha b^\alpha ,\quad (\frac{a}{b})^\alpha =\frac{a^\alpha}{b^\alpha}$$
其中 $a,b$ 是正实数， $\alpha,\beta$ 是任意实数。
对数运算法则
- $$ \log_a(MN)=\log_aM + \log_aN (积的对数=对数的和)$$
- $$ \log_a\frac{M}{N}=\log_aM - \log_aN (商的对数=对数的差)$$
- $$ \log_aM^n=n\log_aM (幂的对数=对数的倍数)$$
- $$ \log_a\sqrt[n]{M}=\frac{1}{n}\log_nM$$
一元二次方程基础
- 一元二次方程 $$ax^2+bx+c=0(a\ne 0)$$
- 根的公式 $$x_{1,2}=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$$
- 根与系数的关系（韦达定理） $$x_1+x_2=-\frac{b}{a},x_1x_2=\frac{c}{a}$$
- 判别式 $$\delta =b^2-4ac,
\begin{cases}
\delta >0, & 方程有两个不等的实根 \[2ex]
\delta =0, & 方程有两个想等的实根 \[2ex]
\delta <0, & 方程有两个共轭等的复根 \[2ex]
\end{cases}
$$ - 抛物线 $y=ax^2+bx+c$ 的顶点 $(-\frac{b}{2a},c-\frac{b^2}{4a})$
因式分解公式
- $$(a+b)^2=a^2+2ab+b^2$$
- $$(a-b)^2=a^2-2ab+b^2$$
- $$(a+b)^3=a^3+3a^2b+3ab^2+b^3$$
- $$(a-b)^3=a^3-3a^2b+3ab^2-b^3$$
- $$(a+b)(a-b)=a^2-b^2$$
- $$a^3-b^3=(a-b)(a^2+ab+b^2)$$
- $$a^3+b^3=(a+b)(a^2-ab+b^2)$$
- $$a^n-b^n=(a-b)(a^{n-1}+a^{n-2}b+\dots +ab^{n-2}+b^{n-1})(n是正整数)$$
- $$n是正偶数时，a^n-b^n=(a+b)(a^{n-1}-a^{n-2}b+\dots +ab^{n-2}-b^{n-1})$$
- $$n是正偶数时，a^n+b^n=(a+b)(a^{n-1}-a^{n-2}b+\dots -ab^{n-2}+b^{n-1})$$
- 二项式定理 $$(a+b)^n=\sum_{k=0}^{n} \mathrm{C}_n^k a^kb^{n-k}=a^n+na^{n-1}+\frac{n(n-1)}{2!}a^{n-2}b^2+\dots + \
\frac{n(n-1)\dots (n-k+1)}{k!}a^{n-k}b^k+\dots +nab^{n-1}+b^n$$
阶乘与双阶乘
- $$n!=1\times 2\times 3\times \dots \times n,规定0!=1$$
- $$(2n)!!=2\times 4\times 6\times \dots \times(2n)=2^n\cdot n!$$
- $$(2n-1)!!=1\times 3\times 5\times \dots \times(2n-1)$$
排列组合数
排列数
$$A^m_n=\frac{n!}{(n-m)!}$$
组合数
$$C^m_n=\frac{A^m_n}{m!}=\frac{n!}{m!(n-m)!}$$
线代
矩阵
伴随矩阵
- $$AA^*=A^*A=|A|E$$
- $$|A^*|=|A|^{n-1},|A|\ne 0$$
- $$(KA)^=K^{n-1}A^$$
- 设 $A,B$ 分别为 $m,n$ 阶可逆矩阵，且 $|A|=a,|B|=b$ ,则
$$
\left(\begin{array}{cc}
A & O \
O & B
\end{array} \right)^{}=
\left|\begin{array}{cc}
A & O \
O & B
\end{array} \right| \cdot
\left(\begin{array}{cc}
A & O \
O & B
\end{array} \right)^{-1}=ab\left(\begin{array}{cc}
A^{-1} & O \
O & B^{-1}
\end{array} \right)=
\left(\begin{array}{cc}
bA^ & O \
O & aB^*
\end{array} \right)$$
$$\left(\begin{array}{cc}
O & A \
B & O
\end{array} \right)^{}=
\left|\begin{array}{cc}
O & A \
B & O \end{array} \right| \cdot
\left(\begin{array}{cc}
O & A \
B & O
\end{array} \right)^{-1}=(-1)^{mn}ab
\left(\begin{array}{cc}
O & B^{-1} \
A^{-1} & O
\end{array} \right)=(-1)^{mn}
\left(\begin{array}{cc}
O & aB^ \
bA^* & O
\end{array} \right)$$
初等矩阵的逆
- $$[E_i(k)]^{-1}=E_i(\frac{1}{k})$$
- $$E_{ij}^{-1}=E_{ij}$$
- $$[E_{ij}(k)]^{-1}=E_{ij}(-k)$$
实对称矩阵
若$A$为实对称矩阵：
则$A^T、A^*、A^{-1}$均为实对称矩阵。
两实对称矩阵的线性和还是实对称矩阵，两实对称矩阵的积不一定为实对称矩阵。
矩阵的秩
- $$P,Q可逆，则 r(A)=r(PA)=r(AQ)=r(PAQ)$$
设 $A$ 是 $m\times n$ 阶矩阵， $B$ 满足有关矩阵运算要求的矩阵，则
2. $$r(A)\le min [m,n] $$
3. $$r(A)=r(A^T)=r(A^TA)=r(AA^T)$$
4. $$r(A\pm B)\le r(A)+r(B)$$
5. $$r(kA)=r(A)(k\ne 0)$$
6. $$r(AB)\le min [r(A),r(B)]$$
7. $$r(AB)\ge r(A)+r(B)-n$$
8. $$AB=O 时，r(A)+r(B)\le n,n是A的列数（或B的行数）$$
9. $$r
\left(\left[ \begin{array}{cc}
A & O \
O & B
\end{array} \right]\right)
=r(A)+r(B)
$$
10. $$r(A)+r(B)\le r
\left(\left[ \begin{array}{cc}
A & O \
C & B
\end{array} \right]\right)
=r(A)+r(B)+r(C)$$
11. $$r(A^*)=
\begin{cases}
n, & r(A)=n \
1, & r(A)=n-1 \
0, & r(A)< n-1
\end{cases}
，其中A为n阶方阵
$$
常用特征值、特征向量
| 矩阵 | $A$ | $kA$ | $A^k$ | $f(A)$ | $A^{-1}$ | $A^*$ | $P^{-1}AP$ |
|---|---|---|---|---|---|---|---|
| 特征值 | $\lambda$ | $k\lambda$ | $\lambda^k$ | $f(\lambda)$ | $\frac{1}{\lambda}$ | $\frac{ \vert A\vert }{\lambda}$ | $\lambda$ |
| 对应的特征向量 | $\xi$ | $\xi$ | $\xi$ | $\xi$ | $\xi$ | $\xi$ | $P^{-1}\xi$ |
$A^T$的特征值与$A$相同，但特征向量不再是$\xi$。
向量组
增加向量个数，增加相关性
增加向量维数，增加无关性
向量个数大于向量维数则必相关
判定条件
矩阵等价
$$A,B同型:A等价B\iff r(A)=r(B)$$
向量组等价
$$向量组A、B等价 \iff 向量组A、B可相互表示,即r(A)=r(B)=r(A|B)=r(B|A)$$
矩阵相似
$$A,B同型、特征值相同、均可对角化 \Longrightarrow A、B相似$$
矩阵A、B相似推论：
$$A^{-1} \sim B^{-1} $$
$$A^{T} \sim B^{T}$$
$$A+A^{-1} \sim B+B^{-1}$$
矩阵合同
$$A、B合同 \iff A、B惯性系数相同$$
关系
$$正定 \Longrightarrow 可逆$$
$$实对称、相似 \Longrightarrow 合同 $$
$$A、B相似 \Longrightarrow r(A)=r(B)、|A|=|B|、|\lambda E-A |=|\lambda E-B|、特征值相同 \Longrightarrow 等价$$
- 《2019张宇高等数学18讲》
- 《2019张宇线性代数9讲》
- 《同济大学高等数学第七版》
