机器学习基础理论：KNN

KNN概述

  kNN（k-NearestNeighbor）算法是一种有监督的基本分类与回归方法，我们这里只讨论分类问题中的 kNN算法。

  kNN算法的输入为实例的特征向量，对应于特征空间的点；输出为实例的类别，可以取多类。kNN算法假设给定一个训练数据集，其中的实例类别已定。分类时，对新的实例，根据其 k 个最近邻的训练实例的类别，通过多数表决等方式进行预测。因此，k近邻算法不具有显式的学习过程。

  kNN算法实际上利用训练数据集对特征向量空间进行划分，并作为其分类的“模型”。 k值的选择、距离度量以及分类决策规则是k近邻算法的三个基本要素。训练数据集的好坏直接决定了KNN模型的好坏。

---

KNN 原理

KNN 工作原理

1. 假设有一个带有标签的样本数据集（训练样本集），其中包含每条数据与所属分类的对应关系。
2. 输入没有标签的新数据后，将新数据的每个特征与样本集中数据对应的特征进行比较。
   1. 计算新数据与样本数据集中每条数据的距离。
   2. 对求得的所有距离进行排序（从小到大，越小表示越相似）。
   3. 取前 k （k 一般小于等于 20 ）个样本数据对应的分类标签。
3. 求 k 个数据中出现次数最多的分类标签作为新数据的分类。

---

KNN 通俗理解

  给定一个训练数据集，对新的输入实例，在训练数据集中找到与该实例最邻近的 k 个实例，这 k 个实例的多数属于某个类，就把该输入实例分为这个类。

---

KNN 算法特点

优点:

• 精度高
• 对异常值不敏感
• 无数据输入假定
• 超参数少
• 无显式训练过程
• 对于类域交叉的时候，KNN比其他算法效果更好，因为它不是根据类域的划分来进行预测的

缺点:

• 计算复杂度高
• 空间复杂度高
• 对稀有的数据无法正确预测

适用数据范围: 数值型和标称型

  在监督学习（supervised learning）的过程中，只需要给定输入样本集，机器就可以从中推演出指定目标变量的可能结果。监督学习相对比较简单，机器只需从输入数据中预测合适的模型，并从中计算出目标变量的结果
  监督学习一般使用两种类型的目标变量：标称型和数值型

标称型：标称型目标变量的结果只在有限目标集中取值，比如真与假(标称型目标变量主要用于分类)
数值型：数值型目标变量则可以从无限的数值集合中取值，如0.555，666.666等 (数值型目标变量主要用于回归分析)

---

SVM和KNN的区别

• KNN根据一个样本点周围的点所属的类别来划分这个样本点的类别，而SVM是在两个类别的边界处，找到一条到所有支持向量的距离最大的分界线。svm通过核函数也可以划分非线性的类别。
• KNN不需要训练，只需要计算，所以数据量大的时候，效率很低，而SVM是需要根据数据来训练出一个最好的分界线。

---

KNN实战——海伦约会

数据集文件：

• datingTestSet.txt
• datingTestSet.csv

数据观察

  数据集总共有1000条数据，无缺失值，包含三个特征：

• 每年获得的飞行常客里程数（0—91273）
• 玩视频游戏所耗时间百分比（0.0—20.919349）
• 每周消费的冰淇淋公升数（0.001156—1.695517）

  标签包含以下三类：

• 不喜欢的人
• 魅力一般的人
• 极具魅力的人

0    40920   8.326976  0.953952  largeDoses
1    14488   7.153469  1.673904  smallDoses
2    26052   1.441871  0.805124   didntLike
3    75136  13.147394  0.428964   didntLike
4    38344   1.669788  0.134296   didntLike
5    72993  10.141740  1.032955   didntLike

数据可视化

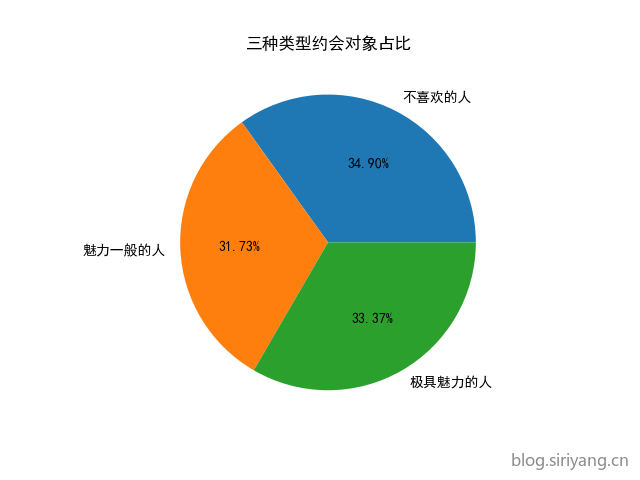
  标签占比圆饼图:

plt.title("三种类型约会对象占比")
plt.pie([342,311,327],labels=["不喜欢的人","魅力一般的人","极具魅力的人"])
plt.show()

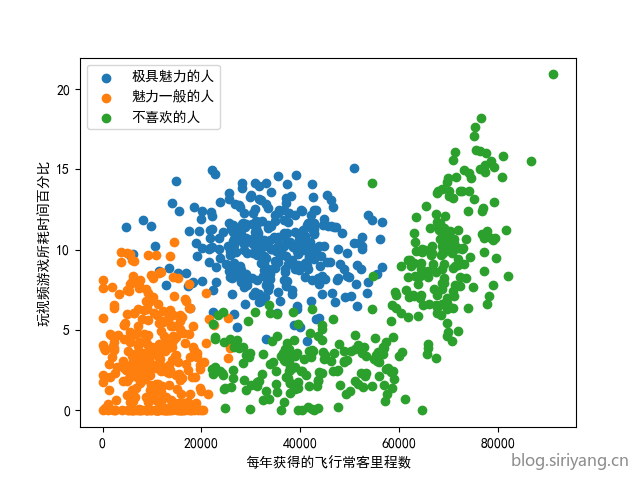
  对前两个特征做散点图：

fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(dataset[dataset[3] == 1][0], dataset[dataset[3] == 1][1],label="极具魅力的人")
ax.scatter(dataset[dataset[3] == 2][0], dataset[dataset[3] == 2][1],label="魅力一般的人")
ax.scatter(dataset[dataset[3] == 3][0], dataset[dataset[3] == 3][1],label="不喜欢的人")
ax.legend(loc='upper left')
ax.set_xlabel("每年获得的飞行常客里程数")
ax.set_ylabel("玩视频游戏所耗时间百分比")
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.show()

---

数据预处理

• 将标签字段由字符串类型替换为整数

dataset.replace(['largeDoses','smallDoses','didntLike'],[1,2,3],inplace=True)

• 对特征值进行线性归一化

0    0.448325  0.398051  0.562334  0.0
1    0.158733  0.341955  0.987244  0.5
2    0.285429  0.068925  0.474496  1.0
3    0.823201  0.628480  0.252489  1.0
4    0.420102  0.079820  0.078578  1.0
5    0.799722  0.484802  0.608961  1.0

---

算法实现

import pandas as pd
import numpy as np

def autoNorm(dataSet):
    """
    Desc:
        归一化特征值，消除特征之间量级不同导致的影响
    parameter:
        dataSet: 数据集
    return:
        归一化后的数据集 normDataSet. ranges和minVals即最小值与范围

    归一化公式:
        Y = (X-Xmin)/(Xmax-Xmin)
        其中的 min 和 max 分别是数据集中的最小特征值和最大特征值。
        该函数可以自动将数字特征值转化为0到1的区间。
    """
    # 计算每种属性的最大值、最小值、范围
    minVals = dataSet.min(0)
    maxVals = dataSet.max(0)
    # 极差
    ranges = maxVals - minVals
    normDataSet = np.zeros(np.shape(dataSet))
    m = dataSet.shape[0]
    # 生成与最小值之差组成的矩阵
    normDataSet = dataSet - np.tile(minVals, (m, 1))
    # 将最小值之差除以范围组成矩阵
    normDataSet = normDataSet / np.tile(ranges, (m, 1))  # element wise divide
    return normDataSet, ranges, minVals

def knnClassify(inX, dataSet, labels, k):
    dataSetSize = dataSet.shape[0]
    # 距离度量 度量公式为欧氏距离
    diffMat = np.tile(inX, (dataSetSize, 1)) - dataSet
    sqDiffMat = diffMat ** 2
    sqDistances = sqDiffMat.sum(axis=1)
    distances = sqDistances ** 0.5

    # 将距离排序: 从小到大
    sortedDistIndicies = distances.argsort()
    # 选取前K个最短距离， 选取这K个中最多的分类类别
    classCount = {}
    for i in range(k):
        voteIlabel = labels[sortedDistIndicies[i]]
        classCount[voteIlabel] = classCount.get(voteIlabel, 0) + 1
    sortedClassCount = sorted(classCount.items(), key=lambda x:x[1], reverse=True)
    return sortedClassCount[0][0]

def getScore(test_y,pred_y):

    precis=0

    for i in range(len(test_y)):
        if(test_y[i]==pred_y[i]):
            precis+=1
    return  precis/len(test_y)

if __name__ == '__main__':
    # 读取数据
    dataset=pd.read_csv("./datingTestSet.csv",header=None)
    dataset.columns = ["fly", "game", "icecream", "label"]

    # 数据预处理
    dataset.replace(['largeDoses','smallDoses','didntLike'],[1,2,3],inplace=True)

    dataset,_,_ = autoNorm(dataset)

    # 划分数据集
    dataset = dataset.sample(frac=1).reset_index(drop=True)
    data_train = dataset.loc[:599].reset_index(drop=True)
    data_test = dataset.loc[600:].reset_index(drop=True)
    train_X, train_Y = data_train.drop(["label"], axis=1), data_train["label"]
    test_X, test_Y = data_test.drop(["label"], axis=1), data_test["label"]

    # 预测
    pred_y = []
    for i in range(400):
        res = knnClassify(test_X.loc[i], train_X, train_Y, 40)
        pred_y.append(res)

    # 计算精度
    print("precis is:",getScore(test_Y,pred_y))

输出结果：

precis is: 0.9575

---

参考资料

• AiLearning 第2章 k-近邻算法